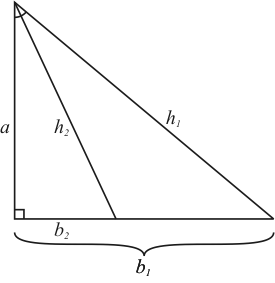
In Figure 1, we have two right triangles, (a, b1, h1) and (a, b2, h2). Both triangles share the same adjacent side a. The triangle (a, b1, h1) has a angle of 40°, which is exactly twice the angle of triangle (a, b2, h2), which has a angle of 20°. Let's say that you know h1 and b1 of the triangle, and you would like to know h2 and b2. What is the relationship between b1 and b2? How about h1 and h2? Examining Figure 1, it doesn't appear there is an obvious solution to this question. Although, using Euclidean geometry, it is possible to derive a relation between h1 and h2, and between b1 and b2.
Normally, the double- and half-angle trigonometric identities are typically solved for using Euler's identity, which is
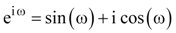 |
Equation 1 |
In Equation 1, 'e' is an irrational number which is the base of the natural logarithm, which is 2.718281828€¦, and the value i is the square root of -1, which is what we call an imaginary number because it doesn't exist. Euler's formula, although it is a powerful tool for doing all sorts of nifty things including providing a shortcut for solving for the double- and half-angle formulas, it doesn't provide an intuitive solution for those who are unfamiliar with the formula. But don't feel dumb, because most people who do use the formula aren't intuitively clear what it means either. So rather than do things the easy way, we will solve for the double- and half-angle formulas geometrically by using good old Euclidean geometry.
The trick we will use to solving for the double- and half-angle formulas is to divide the triangle in Figure 1 into four separate sections (see Figure 2).
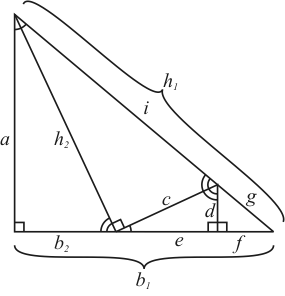
After dividing up the triangle, we now have five right triangles, which are from largest to smallest: (a, b1, h1), (h2, c, i), (a, b2, h2), (e, d, c), and (d, f, g). All corners with single angle mark are 20°, and corners with double angle mark are 70°. Three of the triangles, (a, b2, h2), (h2, c, i), and (e, d, c) are similar triangles, meaning they have the same angles. Because of this, the ratios of the sides for each of these triangles are the same. Therefore, we can state the following:
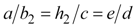 |
Equation 2 |
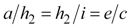 |
Equation 3 |
Also, (a, b1, h1) and (d, f, g) are similar triangles. Therefore,
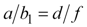 |
Equation 4 |
 |
Equation 5 |
Furthermore, we realize that h1 and b1 can be thought of as the sum of the sides of other triangles.
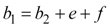 |
Equation 6 |
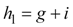 |
Equation 7 |
And finally, since we have right triangles, we have at our disposal ' theorem. For the purposes of this paper, we will only need to use the theorem for the triangles (a, b1, h1) and (a, b2, h2).
 |
Equation 8a |
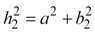 |
Equation 8b |
Equations 2 through 8 provide enough information to derive the half- and double-angle formulas. The first step is to solve for sides c, d, e, f, g, and i in terms of a, b1, b2, h1, and h2. To begin, we can solve for i using equation 3, e using equations 2 and 3, and c and d using equation 2.
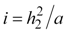 |
Equation 9 |
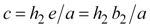 |
Equation 10 |
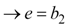 |
Equation 11 |
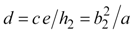 |
Equation 12 |
We can now find f using equations 4, 6, 11, and 12.
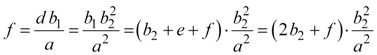 |
|
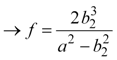 |
Equation 13 |
Similarly, we find g using equations 5, 7, 9, and 12.
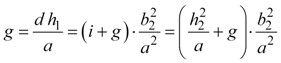 |
|
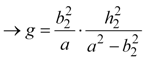 |
Equation 13 |
Finally, we can express b1, b2, h1, and h2 entirely in terms of each other. We can now determine b1 by combining equations 4,12, and 13, and h1 by combining equations 5, 9, 12, and 14.
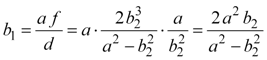 |
Equation 15a |
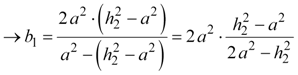 |
Equation 15b |
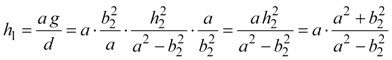 |
Equation 16a |
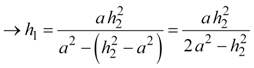 |
Equation 16b |
Using equation 15a and 16a, we can solve for b2 in terms of h1 and b1.
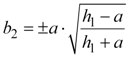 |
Equation 17a |
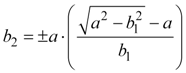 |
Equation 17b |
Finally, we can solve equations 17a and 17b for h2 in terms of h1 and b1.
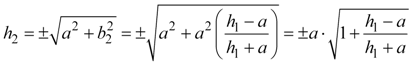 |
|
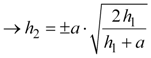 |
Equation 18a |
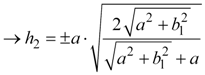 |
Equation 18b |
We now rearrange equations 15 through 18 so they are expressions of ratios of the sides of the triangles, then substitute in the correct trigonometric identities to relate the angle of the triangle. Equations 19, 20, and 21 are the double-angle trigonometric identities, and they fall directly out of equations 15a and 16b. Equation 21 combines equations 19 and 20 using the trigonometric identity sin(θ) = tan(θ) cos(θ).
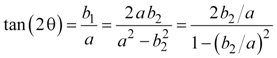 |
Equation 19a |
 |
Equation 19b |
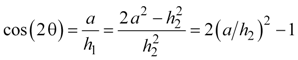 |
Equation 20a |
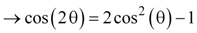 |
Equation 20b |
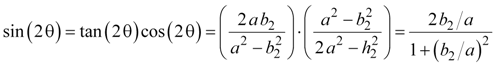 |
Equation 21a |
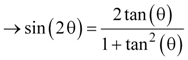 |
Equation 21b |
Equations 23, 24, and 25 are the half-angle trigonometric identities, and they fall directly out of equations 19 and 20. Equation 24 combines equations 22 and 23 using the trigonometric identity sin(θ) = tan(θ) cos(θ).
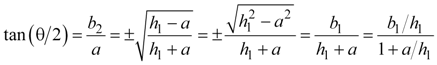 |
Equation 22a |
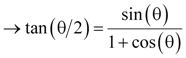 |
Equation 22b |
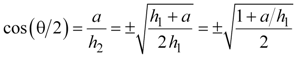 |
Equation 23a |
 |
Equation 23b |
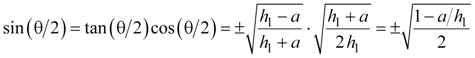 |
Equation 24a |
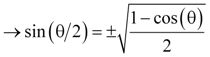 |
Equation 24b |
