Let's say you throw a ball vertically with an initial velocity of v₀ at time t₀. As the ball rises, it slows down due to earth's gravitational pull, eventually reaching a peak distance from the ground, which we will call h₁. At that point, the direction of the ball reverses and it falls back down towards the ground. Finally, the ball strikes the ground at time t₁. Let's say that at that point, the ball undergoes an inelastic collision with the ground, loses energy, and rebounds at velocity v₂ climbing to a height of h₂, which is exactly half of h₁. On the second bounce at time t₂, the ball loses more energy so that it only climbs to a height of h₃, which is half of h₂. The ball continues bouncing losing half its kinetic energy every bounce, and as time progresses, the time between bounces gets smaller and smaller.

Figure 1. Simulation of a bouncing ball.

A simulation of a bouncing ball is illustrated in Figure 1. After around eleven bounces, the height of each bounce is so small you can't see it on the graph anymore. But even then, the ball is still bouncing. The reader is left to ponder: how can we know when the ball stops bouncing? How many times does the ball bounce before it finally comes to rest? Or maybe, that isn't the right question, since it would seem as though the ball can rebound to half its height infinitely many times. But if the ball bounces infinitely many times, doesn't that mean that the ball should never stop bouncing? In this paper, we will explore this subject in depth, and determine when, if ever, the ball stops bouncing by using mathematics.

Developing a Mathematical Model

To begin, I will try to give an intuitive review of the physics equations of motion which apply to the ball. Since the ball can go either of two directions, up or down, we will need to apply physics equations of motion for a 1-dimensional universe. So let's quickly derive the basic physics equations of motion for the ball using integral calculus. In this problem, we will assume that the Earth applies a constant force to the ball despite the distance of the ball from the Earth. This assumption is accurate enough for our analysis since it is impossible for a human being to throw a ball high enough so that the force of gravity between the ball and the earth changes a significant amount. In physics, the letter g is a constant which signifies the acceleration caused by the earth on a dropped object, which is approximately 9.8 m/s². We will also ignore the affects of air resistance on the ball. Using Leibniz differential calculus notation, the velocity and acceleration due to gravity of a falling object are defined using the following equations:

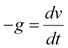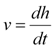Equation 1a,b

Equation 1a states that the acceleration due to Earth's gravitational pull (-g) is the rate of change of velocity (v). Manipulating the equation, we can solve for the velocity as a function of time.



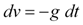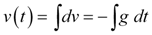	Equation 2

Equation 1b simply states that velocity (v) is the rate of change of the height (h) of an object. Using Equation 2, we can solve for an expression of the height of the object as a function of time.



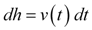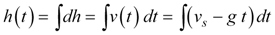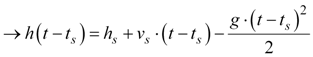	Equation 3

Equations 2 and 3 give the velocity and position of any object with constant acceleration moving in one-dimensional space. The values v_s and h_s are constants produced by the integration, which represent the velocity and height of the object at time t_s. Now that we have equations which relate the height and velocity of the ball, we can use them to analyze the motion of the ball as it is affected by the Earth's gravity. We will begin by analyzing a single bounce of the ball.

Figure 2. Generalized bounce cycle

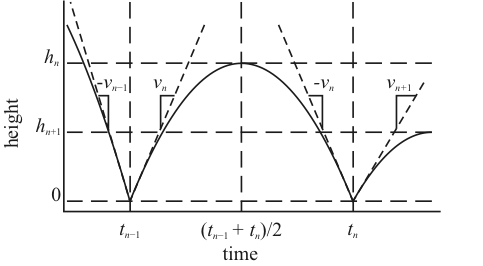
In Figure 2, we see what we will call a 'bounce cycle' spanning from time t_n_‑1 to t_n. At time t_n_‑1, the ball undergoes an inelastic collision with the ground, causing the ball to reverse direction and lose kinetic energy. Half-way through the bounce cycle, the velocity decreases to zero, and at that point, the ball is at the maximum height h_n. This height is related to the maximum height of the previous bounce cycle by the constant r, which is the rebound coefficient defined by r = h_n/h_n_‑1 (we will assume 0 ≤ r < 1). At the end of the cycle, the ball is traveling at a speed of ‑v_n as it once again collides with the ground at time t_n, at which point the next bounce cycle begins. The ball will reach its maximum height h_n at time t_max,n = (t_n_‑1 + t_n)/2. We can find out at what time the ball reaches its maximum (t_max,n) by solving for the time at which the velocity of the ball is zero using Equation 2 with t_s = t_n‑1and v_s = v_n.


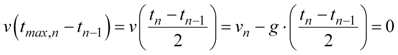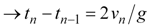	Equation 4

Next, we can then find the ball's maximum height at time t_max,n using Equations 3 and 4 with t_s = t_n‑1, h_s = 0, and v_s = v_n.


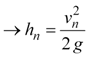	Equation 5

We now have expressions for the duration (Equation 4) and maximum height (Equation 5) of each bounce cycle; however, we prefer to have expressions which state them in terms of the initial velocity v₀. To do so, we first need to solve for the coefficient of restitution. The coefficient of restitution is the ratio of the magnitude of the ball's velocities immediately before and after impact with the ground. Or in general terms, the coefficient of restitution is v_n/v_n_‑1. This is not to be confused with r, which we defined earlier to be the rebound coefficient h_n/h_n_‑1; although, they're related, and we can use r to solve for the coefficient of restitution. To do so, we will set h_n = r h_n_-1 using Equation (5), then solve for v_n/v_n_‑1.


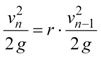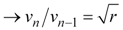	Equation 6

The coefficient of restitution for our ball is therefore the square root of the rebound coefficient r. Using Equation 6, we can find the relation for any rebound velocity v_n to the initial velocity v₀.


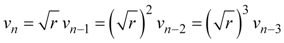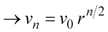	Equation 7

Using this result, we can state the rebound velocity, maximum height, and bounce cycle duration for any one of the bounces in terms of the initial velocity of the ball, v₀. By plugging Equation 7 into Equations 4 and 5, we find:

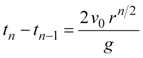	Equation 8
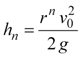	Equation 9

Now that we have an expression for the duration of the bounce cycle, we can begin to add the times up one by one, starting at time t₀. We can calculate the total time until the n^th bounce by adding up the first n bounce cycle times.

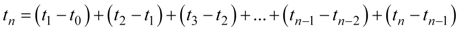Equation 10

Combining Equations 8 and 10, we come up with the following geometric series.


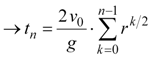	Equation 11

As long as 0 ≤ r < 1, the geometric series in Equation 11 converges to a specific time t_final, at which time the ball is no longer bouncing.

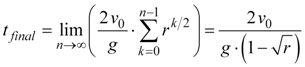Equation 12

The implications of these results are quite profound. Through mathematics, we have shown that after the ball bounces an infinite number of times, it will finally come to a stop at time t_final. Another way of solving for t_final is by performing a 2^nd‑degree polynomial fit using any three peak heights and times as data points. Using the first three peaks, we build up the following matrix.

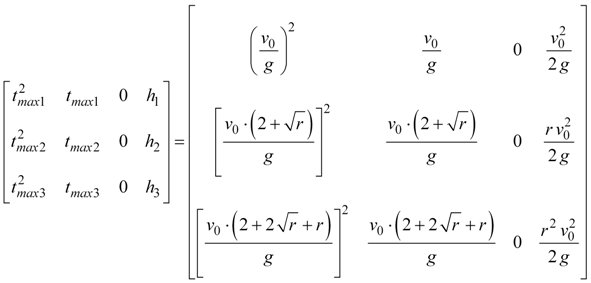Equation 13

Converting Equation 13 to reduced row echelon form results in the following polynomial 2^nd‑degree polynomial fit:

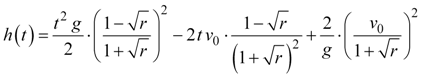Equation 14

This polynomial factors quite nicely into the following expression:

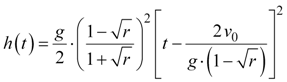Equation 15

As a result, we end up with an equation for a scaled and delayed parabola. By plugging in various values of t_n from Equation 11 into Equation 15, we verify that the results match the expected values of h_n found in Equation 9. Also, it can be easily seen that the value of the function is zero when t is the same value of t_final we found in Equation 12. Figure 3 shows the results of inscribing h(t) onto the waveform of the bouncing ball, showing that it passes directly through all maximum points for all the bounce cycles.

Figure 3. Peak-matching 2^nd degree polynomial h(t) inscribed on bouncing ball waveform

Using both Equations 12 and 15, we can know precisely the time at which a ball with rebound coefficient r and initial upward velocity v₀ will come to a complete stop. For example, if we were to throw a ball with a rebound coefficient r = ½ upward with initial velocity v₀ = 10 m/s, the ball will finally come to rest in 6.97 seconds.

Conclusion

These results provide a disproof of Zeno's paradox, which states that it shouldn't be possible for a runner to complete a race, because he would have to travel half-way to the finish line infinitely many times. Using the example of the bouncing ball, we have shown that it is mathematically possible for someone to watch a ball bounce to half its height an infinite number of times and live to tell about it.